You can’t talk about trigonometry without talking about the Pythagorean Theorem. This is one of the most elegant, simple, beautiful, and useful equations in all of mathematics. It’s used all the time in science and engineering (I make use of it almost every day), and even non-mathochists at least know it by name.

It’s well enough known to be misquoted in popular culture.  Upon receiving his Doctorate of Thinkology diploma from the Wizard of Oz, the Scarecrow proudly shows off his new smarts by saying, “The sum of the square roots of any two sides of an isosceles triangle is equal to the square root of the remaining side. Oh, joy, oh, rapture. I’ve got a brain!”

Except that he was experiencing so much joy and rapture that his brain got it wrong. Three times.

1. The Pythagorean Theorem is concerned with right triangles, not isosceles triangles. An isoscoles triangle is a triangle with 2 sides of the same length. A right triangle, as we have previously explored, is a triangle one of whose angles is a right angle, i.e. a 90-degree angle. Different beasts.
2. The equality is concerned with the squares of the lengths of the sides, not the square roots of the lengths.
3. The equality is very specific about what equals what; you don’t pick “any two sides,” do some mathemagic to them, and expect it to equal whatever mathemagic you do to the third side.

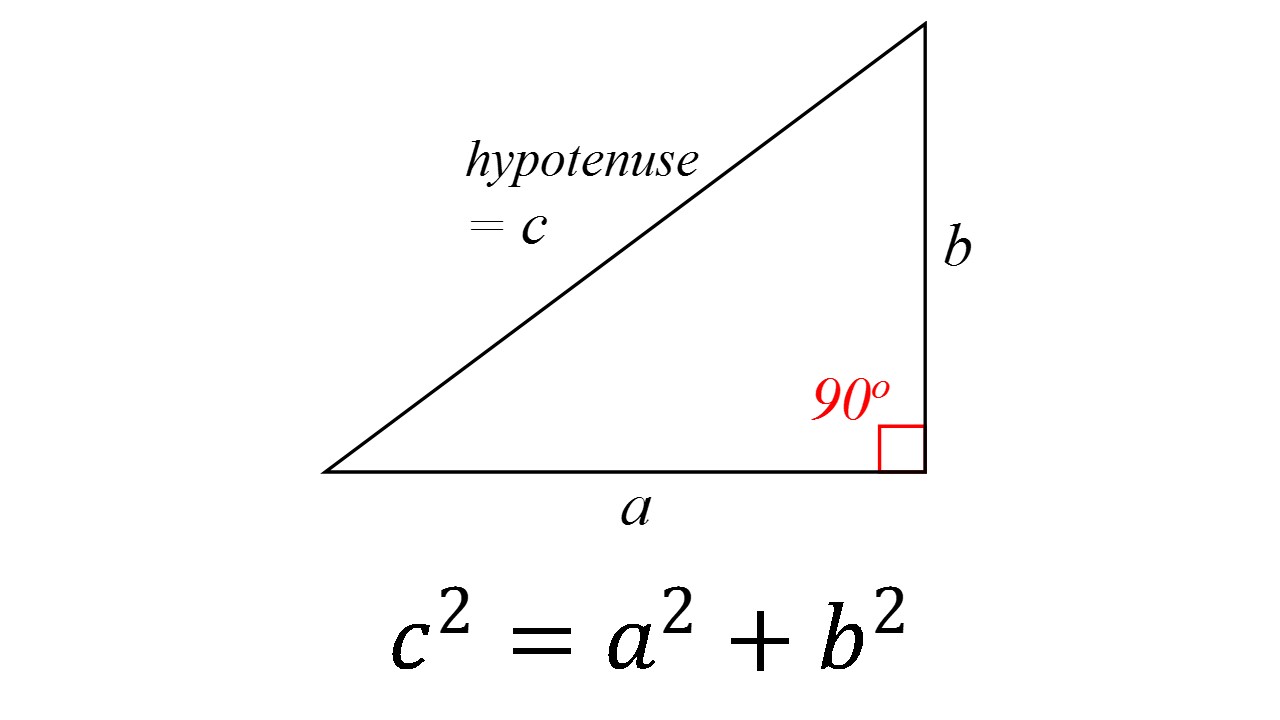
The theorem is illustrated in the picture below. The correct wording is as follows: For a right triangle, the square of the length of the hypotenuse (the longest side, which is opposite the right angle) is equal to the sum of the squares of the lengths of the other two (shorter) sides.

Regarding exponents, i.e. the funny “2” floating above each letter in the picture, see the EXPONENTS page.

The theorem is named after the ancient Greek mathemetician Pythagoras (c. 570 – c. 495 BC). The theorem may well predate him, but tradition credits him as being the first to prove it. The proof is wonderfully elegant and simple. (Contrary to poplular belief that mathochists like everything to be as complicated as possible, we really do like simplicity when we can find it.)

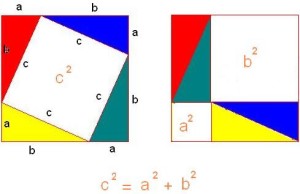
The proof goes like this. Take a square with sides of length c as shown in the picture below, place it inside a larger square, and tilt it so that its corners touch the edges of the larger square. This produces 4 identical triangles (the actual term is “congruent,” for any fellow mathochists who might be grading me) filling in the space between the inner and outer square. The hypotenuse of each of these triangles is c, we’ll call the shorter leg of each triangle “a” and the longer leg “b”.

The area of the square in the left-hand picture, i.e. the white space, is c x c, or c². If we rearrange the colored triangles as shown in the right-hand picture, the white space now consists of two squares, one with sides of length a and the other with sides of length b. The areas of these two squares are, respectively, a x a = a² and b x b = b². The sums of these two areas must equal the are of the original square, i.e. c x c = c², Q.E.D.

Other proofs and more history about the Pythagorean Theorem can be found on the Wikipedia page for the theorem at the link below:

http://en.wikipedia.org/wiki/Pythagorean_theorem